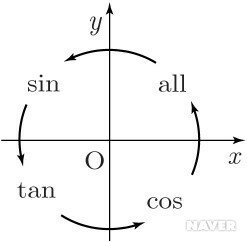
tan 값을 알고 있는 경우, $\theta$가 속해있는 사분면에 따라, 올싸탄코 이용하여 부호를 결정하고 그 부호에 다음을 붙이면 sin, cos을 결정할 수 있다. (단, $\tan\theta=m$) * 올싸탄코(삼각함수의 각변환)의 경우, 다음 참고. 더보기 2023.01.18 - [🏫 Study/수학 I] - [수학 I] 삼각함수의 각 변환 [수학 I] 삼각함수의 각 변환 삼각함수 각 변환 순서 각을 $\frac{n}{2}\pi \pm \theta$꼴로 나타내기 ($n\in \mathbb{Z}$) $n$이 짝수이면 그대로, 홀수이면 아래처럼 고침. sin → cos cos → sin tan → cot (=$\frac{1}{tan}$) 얼싸탄코(얼싸안코; all- scian.xyz $\sin\the..