I. 파동
파동 함수
$y=Asin(kx-\omega t)$ ($A$: 진폭, $k$: 파수, $\omega$: 각진동수)
파수 $k=\frac{2\pi}{\lambda}$
각진동수 $\omega$ (rad/s)
$\omega=\frac{2\pi}{T}=2\pi f$ ($f$: 진동수)
$kv=\frac{2\pi}{\lambda}\cdot\frac{\lambda}{T}=\frac{2\pi}{T}=\omega$ ($\lambda$: 파장)
위상
$(kx-\omega t)$: 위상 (위상각)
위상차가 $\pi$의 짝수 배: 같은 위상 / 홀수 배: 반대 위상
II. 간섭
이중 슬릿 간섭 실험 (by Young)

경로차 ($\Delta$)
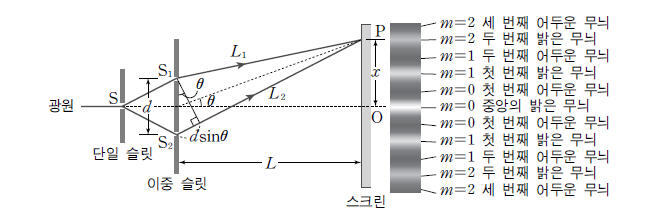
$\Delta=|\overline{S_1P}-\overline{S_2P}|=dsin\theta\approx dtan\theta = \frac{dx}{L}$
간섭 조건
보강간섭: $\Delta=\frac{\lambda}{2}$의 짝수 배
상쇄간섭: $\Delta=\frac{\lambda}{2}$의 홀수 배
이웃한 밝은(어두운) 무늬 사이의 간격
간섭 조건과 구분!!
이웃한 밝은(어두운) 무늬 사이의 간격을 $\Delta x$, 파장을 $\lambda$라 하면,
$\Delta x=\frac{L\lambda}{d}$
박막으로 광로를 가렸을 때 (박막의 굴절률: n)

$y' = \frac{aL}{d}(n-1)$
▶ 무늬 간격은 박막으로 가리지 않았을 때와 같고, 전체적으로 위쪽으로 치우친다.
박막 간섭
🖼 Background // 고정단 반사와 자유단 반사
소한 매질: 굴절률이 작은 매질 (파장 길고, 속도 빠름)
밀한 매질: 굴절률이 큰 매질 (파장 짧고, 속도 느림)
소한 매질 → 밀한 매질 : 고정단 반사 (위상이 $\pi$만큼 변화)
밀한 매질 → 소한 매질 : 자유단 반사 (반사에 따른 위상 변화 X)
박막에서의 광로차 ($\Delta$)
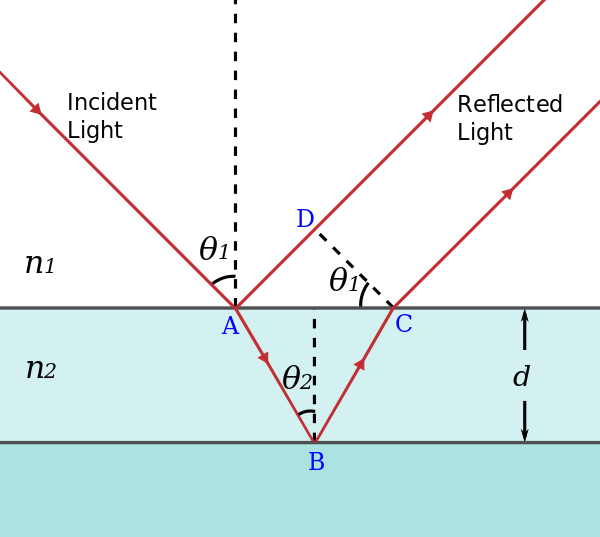
$\Delta = 2ndcos \theta$ ($\Delta$: 광로차, 빛은 굴절률이 $n$인 매질 속에서 이동함)
박막에 의한 빛의 간섭 조건
- 고정단 반사가 1회 일어날 때
보강 간섭: $\Delta = 2ndcos\theta = \frac{\lambda}{2}(2m+1)$
상쇄 간섭: $\Delta = 2ndcos\theta = \frac{\lambda}{2}(2m)$
($m=0, 1, 2, \cdot\cdot\cdot$) - 고정단 반사가 0회 or 2회 일어날 때
보강 간섭: $\Delta = 2ndcos\theta = \frac{\lambda}{2}(2m)$
상쇄 간섭: $\Delta = 2ndcos\theta = \frac{\lambda}{2}(2m+1)$
($m=0, 1, 2, \cdot\cdot\cdot$)
투과하는 빛의 간섭 조건

쐐기간섭
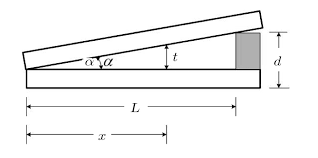
간섭 조건
보강 간섭: $\Delta = 2t = \frac{\lambda}{2}(2m+1)$
상쇄 간섭: $\Delta = 2t = \frac{\lambda}{2}(2m)$
($m=0, 1, 2, \cdot\cdot\cdot$)
$t=\frac{d}{L}x$
간섭무늬 간격 $\Delta x = \frac{\lambda}{2tan\theta}$
Plus. Newton Ring (뉴턴 링)

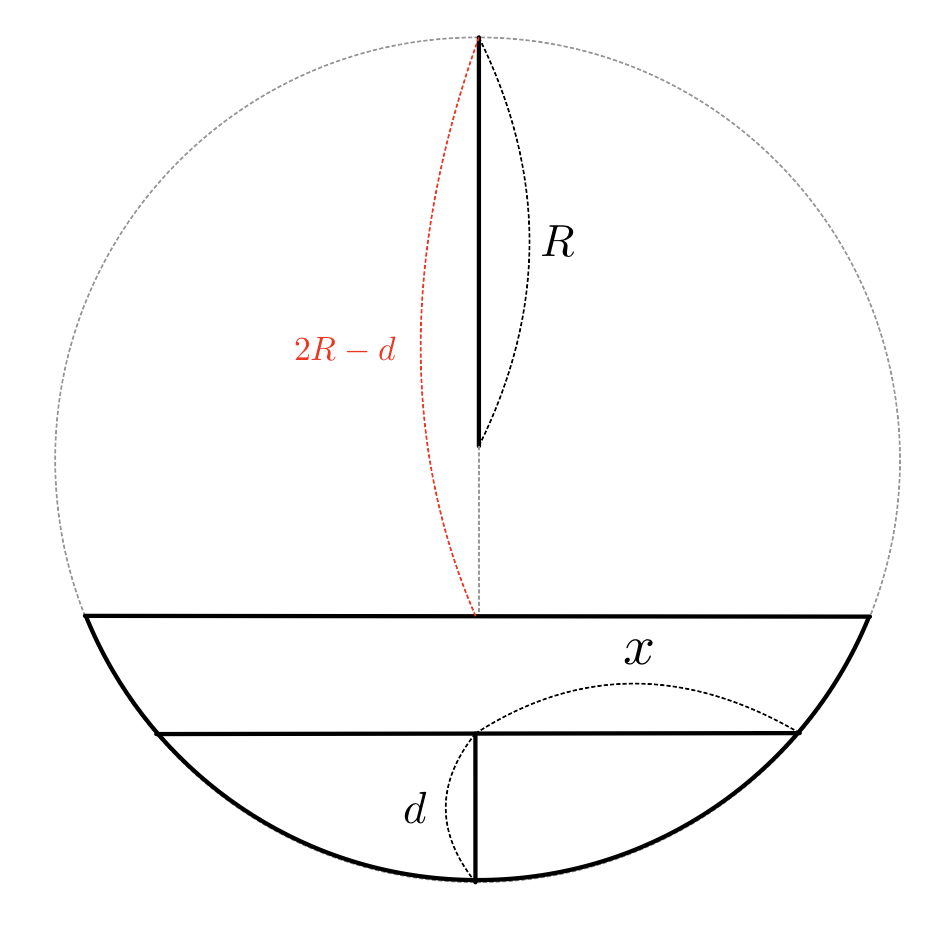
$\Delta = 2d$
보강 간섭: $\Delta = \frac{\lambda}{2}(2m+1)$
상쇄 간섭: $\Delta = \frac{\lambda}{2}(2m)$
$d=\frac{D}{L}x$

