양자역학 (2) - 흑체복사, 자외선 파탄

---

Intro

우리는 일반화학에서 다루는 양자역학 중에서 암기해야 할, Point 부분만을 골라 학습할 것이다.

양자역학 자체가 접하기도 어렵고, 이해하기는 더더욱 어렵기 때문에, 특히 시험을 앞둔 과학고/영재학교생이나 대학생은 암기하는 데 중점을 둘 것을 권장한다. 다만, 본 글에서는 수식적 증명의 과정을 비교적 상세히 작성하여 풀이에도 집중할 수 있도록 하였다.

필자 또한 암기에 도움을 받고자 본 글을 작성한다. 본문은 노트 필기와 비슷한 방식으로 작성될 것이며, 문장보다는 수식 또는 이미지 혹은 개요식의 텍스트가 중점적으로 배치될 것이다. 다만, 필요한 경우 문장으로 풀어서 설명할 수 있다.

앞으로 약 5~6개의 포스팅을 통해 양자역학에 대해 배우게 (암기하게) 될 것이다.

준비가 되었다면, 아래로 스크롤을 내리자!

 

---

* 이전 편 (보어 모형 편)을 보고 오시는 것을 권장드립니다!

2023.02.07 - [🏫 Study/Chemistry] - 양자역학 (1) - 보어 원자모형 (Bohr Model)

양자역학 (1) - 보어 원자모형 (Bohr Model)

 

흑체복사

이번 내용은 실험 결과에 맞춰 만들어진(?) 어느 정도는 끼워 맞춰진 것처럼 보이는 내용이 있어 부자연스러울 수 있으나, 받아들이도록 노력하자. (암기 중점!)

 

흑체

흑체(blackbody)는 이론상 모든 빛을 흡수하여 검게 보이는 물체를 의미한다.

 

열평형과 자외선 파탄

흑체는 열평형 상태에 따라 다음과 같이 파장을 처리한다.

• 열평형 도달 전: 모든 파장의 별을 흡수한다.
• 열평형 도달 후: 모든 파장을 방출(복사)한다.

레일리-진스 법칙과 자외선 파탄(자외파탄)

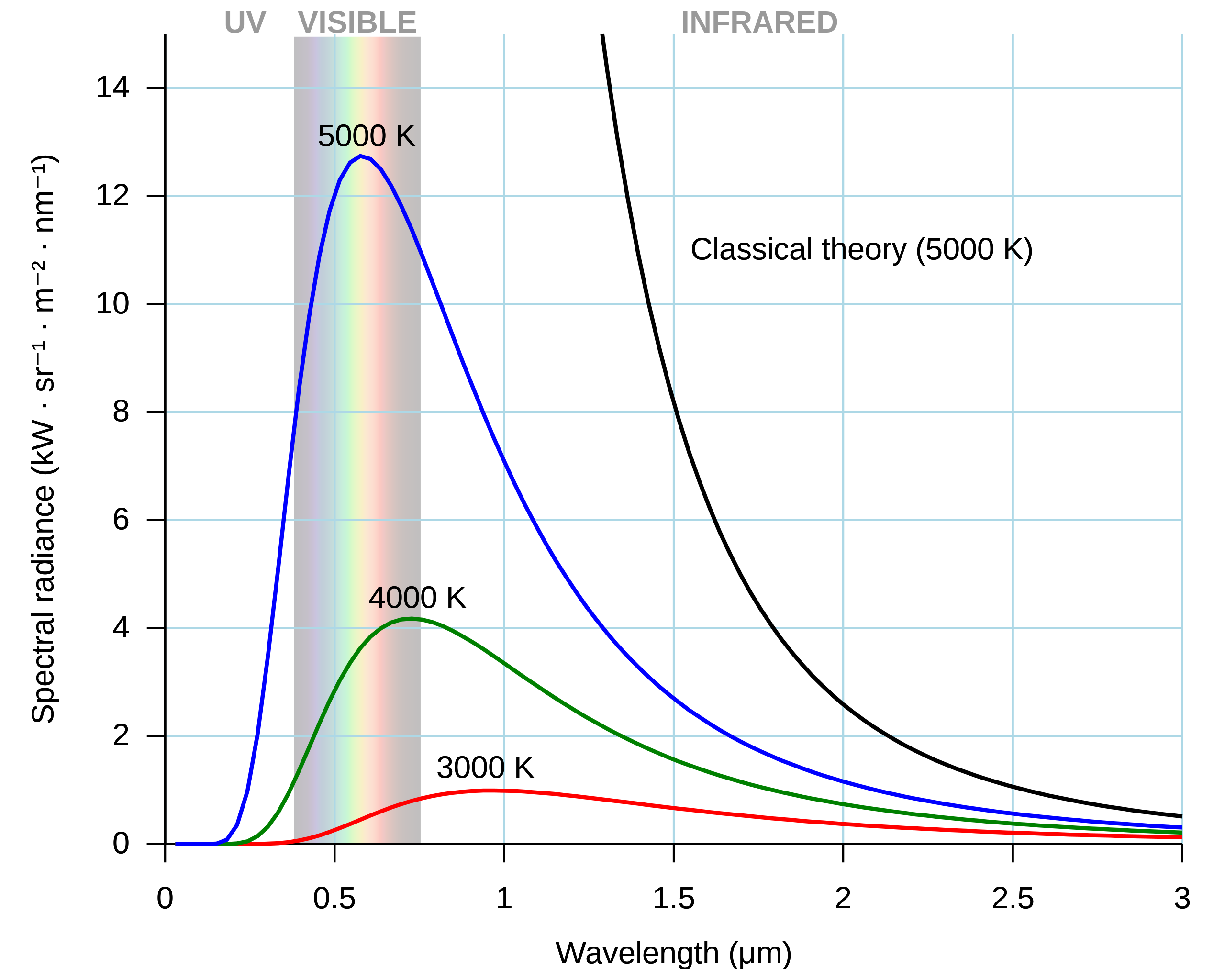
위 그림에서 무지개 색으로 칠해진 부분에서 자외선 파탄(자외파탄이라고도 함.)이 일어난다.

위 그림의 'Classical Theory' 부분이 고전적인 이론에서 '레일리-진스 법칙'에 의해 이상적인 흑체의 복사 에너지를 계산할 때의 그래프인데, 짧은 파장대에서 발생하는 오류를 '자외선 파탄'이라고 한다.

 

흑체에서 방출된 복사선

흑체에서 방출된 복사선은 흑체 온도에 의존하게 된다.

• 흑체 온도가 높으면 → 더 강한 에너지의 빛 방출
  $M=\rho\cdot T^4$ (슈테판-볼츠만 법칙) [$J/m^2\cdot s$: 단위 면적당, 초당 발생하는 에너지 총량]; 여기서는 빛의 세기를 $\rho$로 적음. (시그마로 표현하는 경우가 많기는 함.)
• 흑체 온도가 높으면 → 더 짧은 파장의 빛 방출
  $T\cdot \lambda_{max}=k$ (빈의 변위 법칙)

* 슈테판-볼츠만 법칙과 빈의 변위 법칙은 고등 지구과학 범위이므로 자세한 설명은 생략한다. (필요한 경우 아래 스크랩 및 위키백과 참고 — '더보기' 클릭)

슈테판-볼츠만 법칙: 흑체의 단위 면적당 복사 에너지가 절대 온도의 4제곱에 비례한다는 법칙

슈테판-볼츠만 법칙 - 위키백과, 우리 모두의 백과사전

 

이 때, 흑체 속 진동자(전자기파) 수와 흑체 속에서 방출하는 에너지는 다음과 같다.

레일리-진스 법칙의 식을 미분한 결과와 같으며, 그 자세한 증명 과정에 대해서는 아래 링크된 해외 논문(Deriving the Rayleigh-Jeans Radiation Law)를 참고하도록 하자.

Deriving the Rayleigh-Jeans Radiation Law

 

흑체 속 진동자 수 (dN)

$dN=\frac{8\pi\nu^2}{c^3}d\nu$ (c: 빛의 세기, $\nu$ (누): 진동수)

 

흑체 속 방출하는 에너지

$\rho=dN\times kT$ ($\rho$: 빛의 세기, $k$: 볼츠만 상수)

여기에 위 식의 dN을 대입하면, $\large \rho = \frac{8\pi\nu^2}{c^3}\cdot kT \cdot d\nu$로, 레일리-진스 법칙 식의 미분 결과가 나오게 된다.

이 식에서 문제점을 찾아보자.

 

이 식의 문제점은 파장이 짧아지면 $\nu$ 값이 커지고($\nu$는 진동수로, 고등 물리학 때 배웠던 파장과 진동수 사이의 관계를 떠올리면 된다.), 이에 따라 빛의 세기가 무한히 커진다는 문제가 발생한다. 즉, 자외선 파탄을 설명할 수 없는 문제가 발생하는 것이다!

(장파장인 경우에서는 $\nu$값이 작아지고, 빛의 세기가 0에 수렴하게 되어 장파장은 설명이 가능하다.)

이제, 맥스웰-볼츠만 분포를 적용해 이러한 문제를 처리해 보자.

 

맥스웰-볼츠만 분포의 적용

위에서 구한 $\rho$에 관한 식을 맥스웰-볼츠만 분포와 적절히 섞으면 아래와 같은 식을 도출할 수 있다. (자세한 전개 과정은 넘어가도록 하겠다.)

$\large \rho=\frac{8\pi h\nu^3}{c^3}\left(\frac{1}{e^{h\nu / kt}-1}\right)d\nu$ (본 섹션에서 편의상 '위 식'으로 표현하겠다.)

 

여기서, 파장이 긴 경우와 짧은 경우를 나누어 살펴보자.

장파장에서의 적용

파장이 긴 경우에는, $\nu$ 값이 작아지게 되고, $h\nu\ll kT$가 된다.

이를 위 식에 적용하게 되면, $e^x\simeq 1+x$로 근사할 수 있게 되어 위 식의 괄호 안이 $\frac{kT}{h\nu}$로 근사된다.

이를 다시 위 식에 대입하면,

$\large \rho= \frac{8\pi h\nu^3}{c^3}\times\frac{kT}{h\nu}\cdot d\nu = \frac{8\pi r^2}{c^3}\cdot kT \cdot d\nu$

 

즉, '흑체 속 방출하는 에너지' 섹션에서 봤던 레일리-진스 법칙의 미분식을 다시 볼 수 있다! (장파장은 마찬가지로 설명할 수 있음)

그렇다면, 레일리-진스 법칙의 미분식에서의 자외선 파탄 오류를 설명하기 위해 파장이 짧은 경우를 살펴보자.

 

단파장에서의 적용

단파장에서는 $\nu$ 값이 커지게 된다.

이에, 위 식에서의 괄호 안, 즉 $\left(\frac{1}{e^{h\nu / kt}-1}\right)$이 0에 수렴하게 되고, 이를 위 식에 대입하면

$\rho=0$이 되어, 자외선 파탄을 설명할 수 있게 된다!

 

---

Intermission

이 포스팅에서는 흑체 복사와 자외선 파탄에 대해 알아보았고, 자외선 파탄을 설명하는 방법에 대해 소개하였다.

다음 포스팅에서는 슈뢰딩거의 파동 방정식에 대해 살펴보도록 하겠다.

상당히 수식적인 부분이 많으니 마음의 준비(?)가 필요할 것이다.