함수의 연속과 불연속
다음 조건을 모두 만족 시킬 때, $f(x)$는 $x=a$에서 연속이라 한다.
[1] 함수 $f(x)$는 $x=a$에서 정의되어 있다.
[2] 극한값 $\lim_{x\rightarrow a}f(x)$가 존재한다.
[3] $\lim_{x\rightarrow a}f(x)=f(a)$
⭐️ $f(x)$가 $x=a$에서 연속일 조건 정리 (암기!) ⭐️
▶ 함수값과 극한값이 존재하고, 일치한다.
▶ $\lim_{x\rightarrow a+}f(x)=\lim_{x\rightarrow a-}f(x)=f(a)$
편하게 생각해 보자면,
그래프를 연필로 그릴 때 연필을 떼지 않고 그래프를 쭉 그릴 수 있으면 연속,
연필을 떼야 하면 불연속으로 생각해 볼 수 있다.
($x=a$에서 그래프가 이어져 있으면 연속, 끊어져 있으면 불연속)
|
함수의 불연속 CASE 3가지
|
||
 |
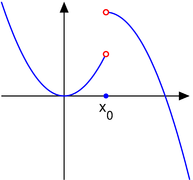 |
 |
|
$f(a)$가 존재하지 않음
|
$\lim_{x\rightarrow a}f(x)$가 존재하지 않음
|
$\lim_{x\rightarrow a}f(x)\neq f(a)$ |

* Image Credit: Erzbischof | Wikimedia Commons
연속함수
구간 (⭐️집합⭐️)
구간은 집합이다!
집합에서 등호가 있으면 닫힌구간, 등호가 없으면 열린구간
| $\{x\mid a\leq x\leq b\}$ | $\{x\mid a\leq x\< b\}$ | $\{x\mid a< x\leq b\}$ | $\{x\mid a< x< b\}$ |
| [a, b] | [a, b) | (a, b] | (a, b) |
| 닫힌구간 | 반닫힌구간 / 반열린구간 | 열린구간 | |
집합에서 부등호가 한개이면,
$\{x\mid x\leq a\}\Leftrightarrow (-\infty ,\ a]$ (무한대는 수가 아니므로 열린구간으로 표현)
실수 전체의 집합은
$\{x\mid$ $x$는 모든 실수 $\}\Leftrightarrow (-\infty ,\ \infty )$
⭐️ $\{x\mid x\neq 3$인 모든 실수$\}$
→ $\{x\mid x< 3 or x>3\}$
→ $\{x\mid x< 3\} \cup \{x\mid x>3\}$
→ (-∞, 3)$\cup$(3, ∞)
함수의 종류별 $f(x)$가 연속인 구간
[1] 다항함수
모든 실수 구간(집합)
[2] 유리함수
{$x\mid$ 분모≠0}
[3] 무리함수
{$x\mid$ 근호 안≥0}
⭐️ 주의!
$\frac{3}{x^2+1}$의 그래프
여기서도 분모가 0이 아니면 연속된 구간이라고 생각할 수 있지만,
x에 어떤 실수가 들어가도 분모가 절대 0이 되지 않으므로 끊어진 구간이 없다!
유리함수라고 해서 모두 끊어진 부분이 있는 것은 아니다!

연속함수의 성질
⭐️⭐️⭐️⭐️ 두 함수 $f(x), g(x)$가 $x=a$에서 (둘 다) 연속이면, ⭐️⭐️⭐️⭐️
아래 함수도 $x=a$에서 연속이다.
* 전제가 중요!!
[1] 실수배
$cf(x)$ (단, c는 상수)
[2] 사칙연산
(1) $f(x)+g(x), f(x)-g(x)$
(2) $f(x)g(x)$
(3) $\frac{f(x)}{g(x)}$ (단, $g(a)\neq 0$)
* 모두 역은 성립하지 않는다!
(위에서 아래로는 가능하지만, 아래서 위로는 성립하지 않는다!)
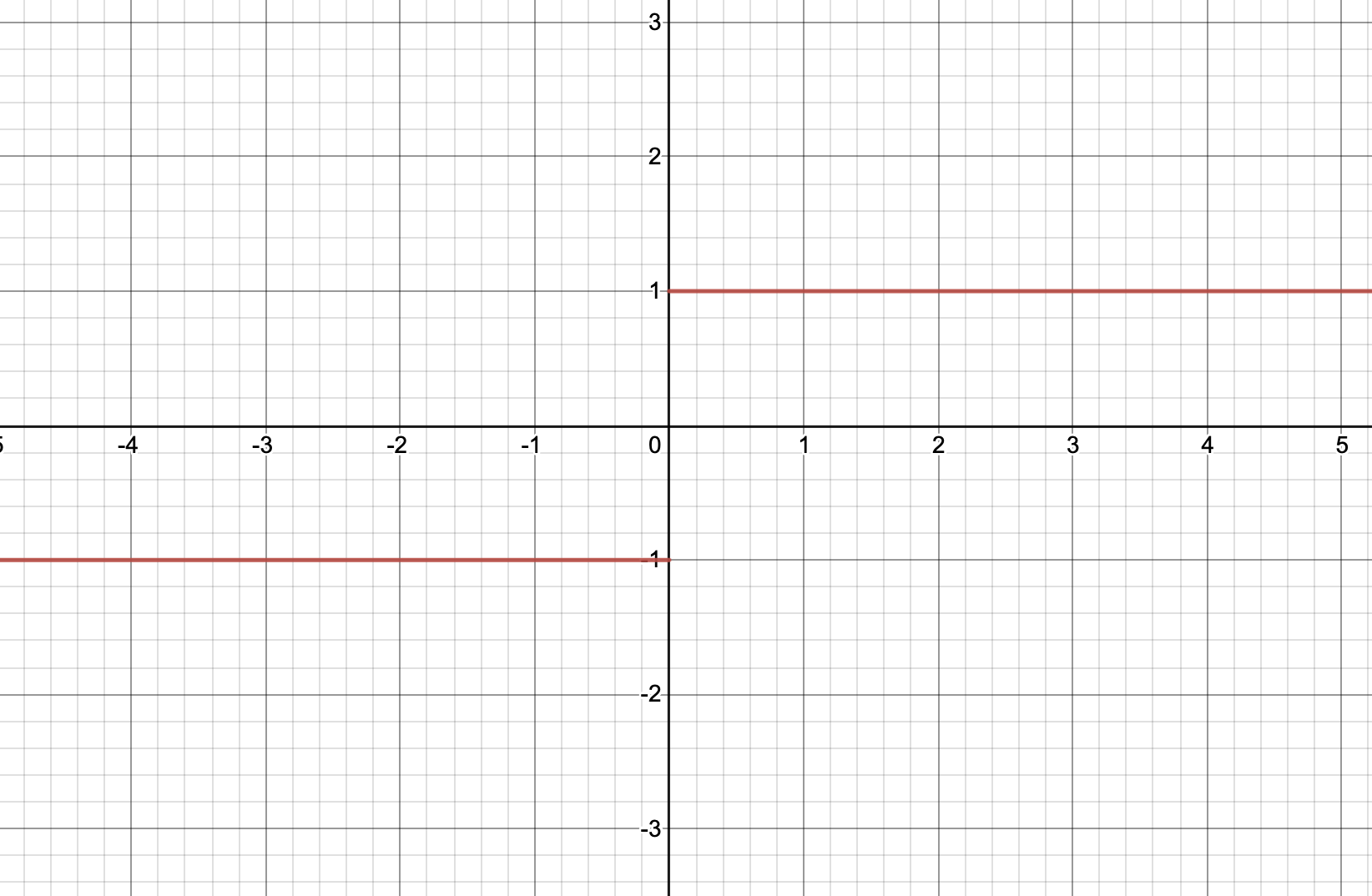
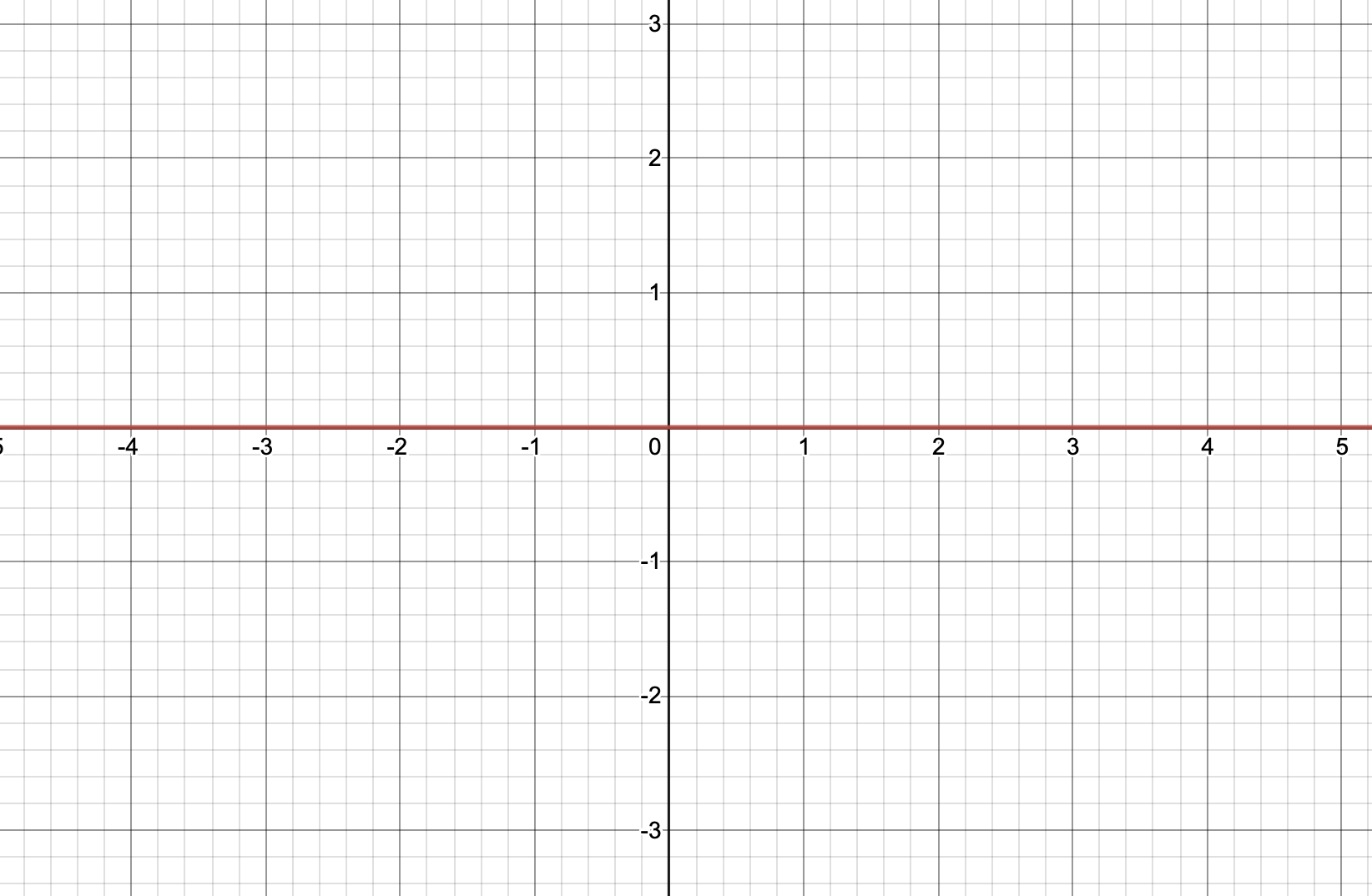
⭐️ 반례 (기억!)
 |
 |
 |
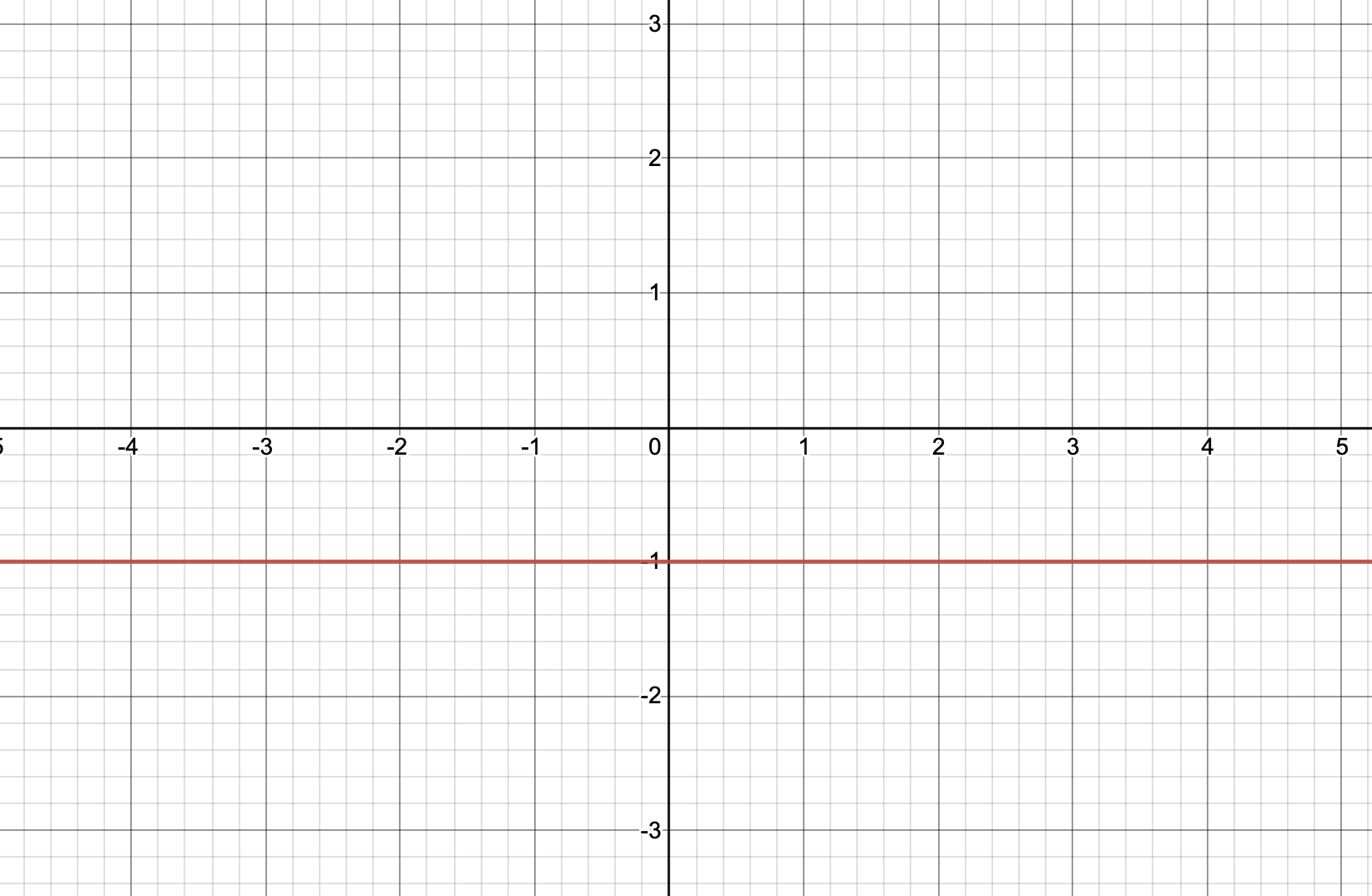 |
| y=f(x) | y=g(x) | f(x)+g(x)=0 | f(x)×g(x)=-1 |

여기서 f(x)와 g(x) 모두 불연속이지만, f(x)+g(x)와 f(x)×g(x) 모두 연속이므로 위의 역은 성립하지 않는다!
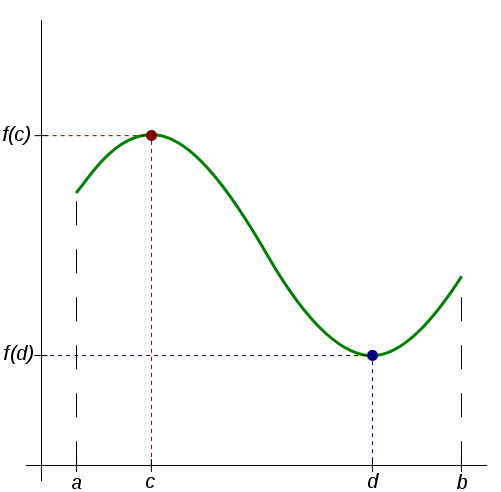
최대·최소 정리
함수 f(x)가 닫힌구간 [a, b]에서 연속이면 f(x)는 이 구간에서 반드시 최댓값과 최솟값을 갖는다.
⭐️ 조건이 중요 ⭐️
조건1) 닫힌구간
조건2) 연속
사잇값의 정리
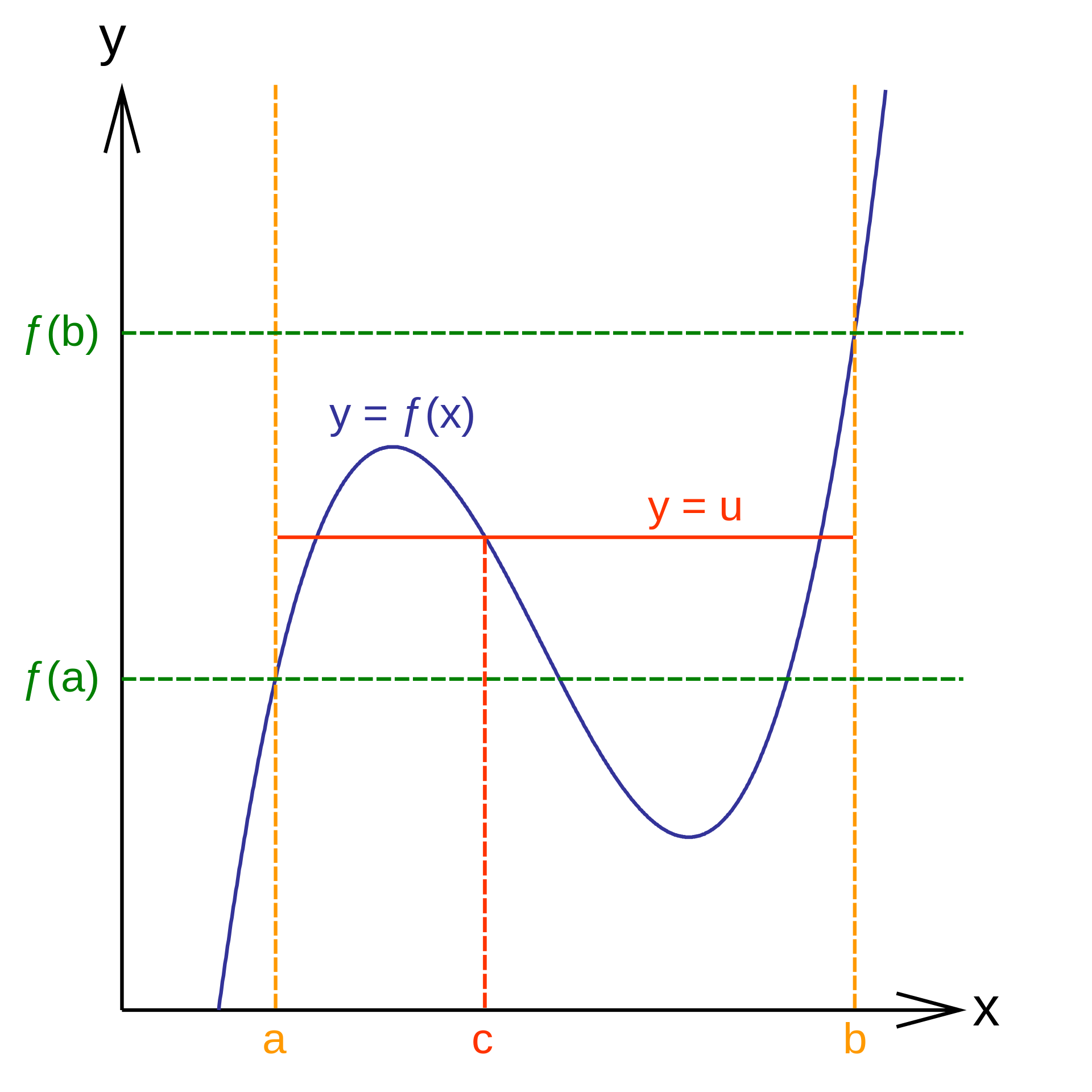
함수 f(x)가 닫힌구간 [a, b]에서 연속이고, f(a)≠f(b)이면 f(a)와 f(b) 사이의 임의의 값 k에 대하여 f(c)=k인 것을 만족하는 실수 c가 a와 b 사이에 적어도 하나 존재한다.
⭐️ 조건이 중요 ⭐️
조건1) 닫힌구간
조건2) 연속
조건3) f(a)≠f(b)
사잇값의 정리의 활용 (응용 ver.)
함수 f(x)가 닫힌구간 [a, b]에서 연속이고, f(a)와 f(b)의 부호가 서로 다르면 (f(a)×f(b)<0),
f(c)=0인 c(방정식의 실근)가 a와 b 사이에 적어도 하나 존재한다.

* Image Credit: Picknick | Wikimedia Commons
사잇값의 정리를 이용하여 f(x)가 연속함수일 때 방정식 f(x)=0의 실근 존재 여부 판별 가능!
|
|
EDITOR: SCIAN https://blog.scian.io/ admin@scian.io IT LOVER | DEVELOPER | ARTIST MATH & SCIENCE |


