미분계수와 도함수 (1) - 평균변화율과 순간변화율, 미분계수

평균변화율 & 순간변화율

증분 ($\Delta$) (구간 [a, x]에서의 증분)

x값의 변화량 x-a를 x의 증분,

y값의 변화량 f(x)-f(a)를 y의 증분이라 하고,

각각 $\Delta x,\ \Delta y$와 같이 나타낸다.

 

평균변화율

함수 y=f(x)에서 x의 값이 a에서 x까지 변할 때의 평균변화율: $\frac{\Delta y}{\Delta x}=\frac{f(x)-f(a)}{x-a}=\frac{f(a+\Delta x)-f(a)}{\Delta x}$ = $\overleftrightarrow{AP}$의 기울기 (평균변화율의 기하적 정의)

순간변화율

순간변화율: $f^\prime (a)=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\lim_{x \rightarrow a}\frac{f(x)-f(a)}{x-a}=\lim_{\Delta x \rightarrow 0}\frac{f(a+\Delta x)-f(a)}{\Delta x}$ (평균변화율에 극한 붙인 것!)

▶ x=a에서의 미분계수

 

미분계수의 기하적 의미

함수 f(x)에서의 x=a에서의 미분계수 $f^\prime (a)$는 곡선 $y=f(x)$ 위의 점 $(a,f(a))$에서의 접선의 기울기와 같다.

$y=x^2$에서 (1,1)의 접선의 기울기

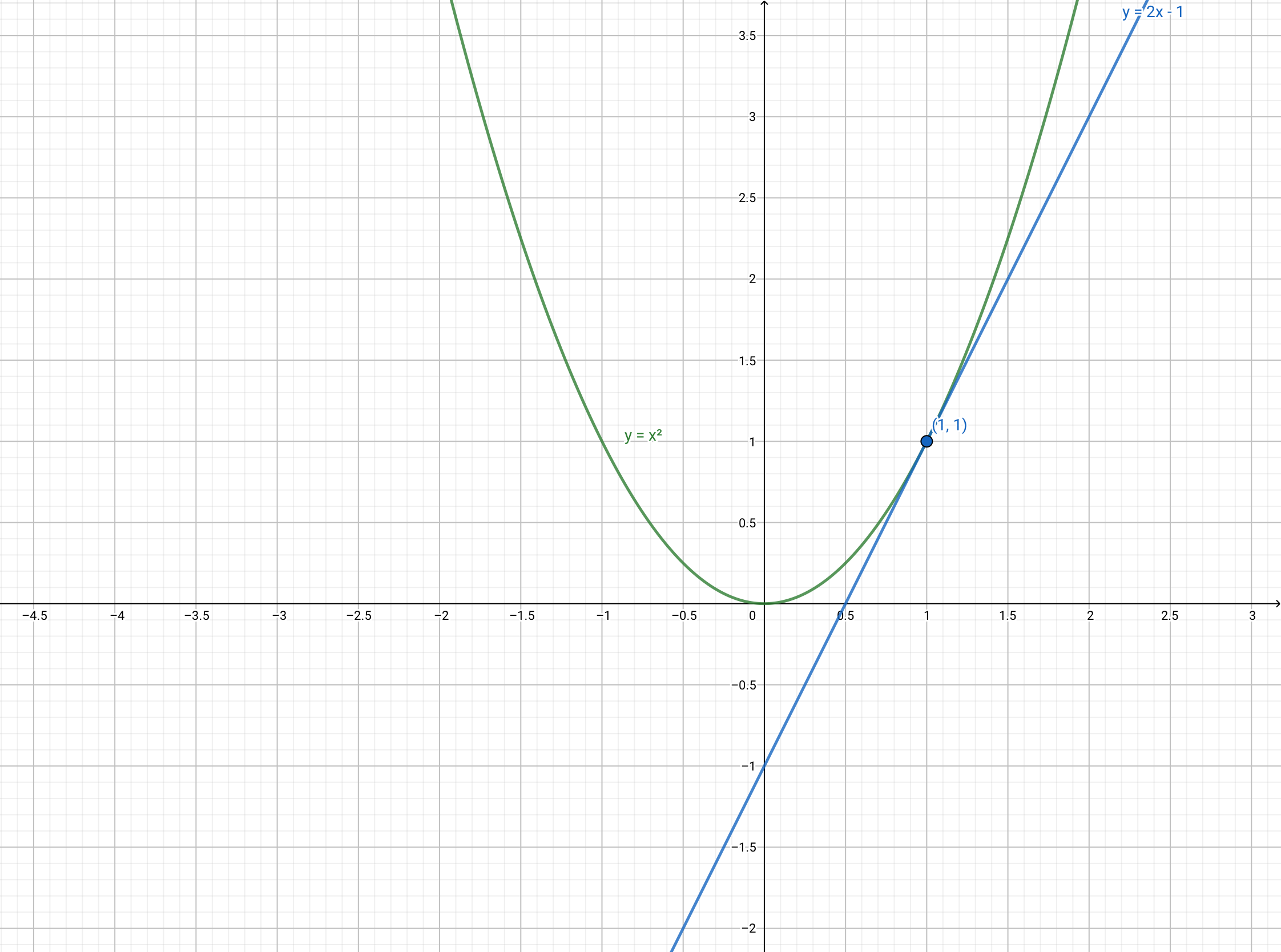
위 그림을 보면, (1,1)의 접선의 기울기는 2이다.

따라서, $f^\prime (1)=2$가 된다.

 

[a, a+h] 구간에서의 증분

[a,a+h] 구간에서의 증분

x가 a에서 a+h까지 변할 때 평균변화율: $\frac{f(a+h)-f(a)}{h}$

순간변화율: $\lim_{h \rightarrow 0}\frac{f(a+h)-f(a)}{h}=f^\prime (a)$

 

 

⭐️ POINT!

평균변화율 vs 순간변화율 구분!

[a, x] 구간과 [a, a+h] 구간 암기!

---

EDITOR: SCIAN https://blog.scian.io/ admin@scian.io IT LOVER | DEVELOPER | ARTIST MATH & SCIENCE